MashPlant的笔记

“你将孤单度过一生”

0%

Earley算法和实现

Posted on Edited on Views: Valine:

Earley算法，是一个parser，所以它的功能也不用我多说了。我第一次接触到它是在看rustc-dev-guide中的macro-expansion这一章时，得知Rust中宏调用的解析是基于Earley算法的。

我自己尝试实现了一下Earley算法，代码：https://github.com/MashPlant/earley。前端演示：https://mashplant.online/earley/

简介

算法的基本信息在wiki上面都有，我这里就简单复述一下。

Earley算法可以解析任何CFG，就像我们自动机课上学的CYK算法一样。Earley parser对于确定性不同的CFG时间复杂度不同，一般情况下是输入长度的立方(这与CYK算法是一致的)，对于无歧义的CFG是平方，对于确定性的(即是某终态接受DPDA的语言，也即是LR(n)语言)CFG是线性。

wiki上面介绍了Earley recognizer的实现，recognizer和parser的区别在于前者只是判断一个输入串是否属于给定的语言，而后者还要解析出输入串的语法树。有一句话让我很不满意：

The recogniser can be easily modified to create a parse tree as it recognises, and in that way can be turned into a parser.

实际上从我的实现来看，把recognizer拓展成parser占据了绝大多数时间和代码量。Jay Earley最初的论文An Efficient Context-Free Parsing Algorithm(这个太长了，我没读过)中提出的把recognizer拓展成parser的方法被指出是有错误的，现在比较正统的方法应该是论文SPPF-Style Parsing From Earley Recognisers中提出的，可惜的是我读了一会，感觉读不懂。

最终我的实现基本上都是参照于http://loup-vaillant.fr/tutorials/earley-parsing/。感觉这个人的文章写的相当不错，能看出他理解的很深刻，风格也算清晰易懂，应该是比我写的好多了，推荐大家去读一下。

Earley recognizer

首先定义Earley item：一个LR(0) item和一个整数的元组，当然也可以看成一个产生式，两个整数的三元组。其中的LR(0) item与LR算法中的意义一致，产生式表示正在解析的产生式，点的位置表示左边的串已经完成解析；还有一个整数，它表示这个产生式是从输入串的这个下标处开始解析的。一个Earley item表示如下：

1
(X -> α • β, start)

设输入串的下标从0开始，输入串的长度是N，为[0, N]每个位置维护一个Earley item的集合，用S[i]表示。S[i]的含义是完成读入了输入串的[0, i)后发现的所有Earley items。S[i]中一个上面那样的Earley item表示的意思就是，正在尝试把输入串的[start, i)这一段解析成X，已经解析了其中的α部分。

算法的核心就是执行一个类似DP的过程，这个伪代码长的有点像Rust，具体语义不难想象：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
S = [{}; N + 1]
// 将`S[0]`初始化成所有`(Start -> • γ, 0)`的集合，Start是初始非终结符，即想要解析的非终结符
// 表示从0开始解析Start，目前还什么都没有解析
for (Start -> γ) in grammar {
  S[0].add((Start -> • γ, 0))
}
for i in 0..=N {
  t = input.get(i) // get对于越界的i(当i = N时)返回None
  for item in S[i] {
    match item {
      // 点后是非终结符，predicate规则
      // 对于语法中所有形如B -> γ的产生式，将(B -> • γ, i) (表示从i开始尝试解析B，目前还什么都没有解析)加入S[i]
      (A -> α • B β, _) => for (B -> γ) in grammar { S[i].add((B -> • γ, i)) }
      // 点后是终结符，scan规则
      // 如果输入的对应位置和这个终结符匹配，将(A -> α b • β, x) (即将点往后移动一位)
      (A -> α • b β, x) if t == Some(b) => S[i + 1].add((A -> α b • β, x)),
      // 点后没有内容，complete规则
      // 已知从x到i成功解析了A，那么对于所有从y到x的部分解析结果，可以把x到i这一段接到后面
      // 对于S[x]中所有形如(B -> α • A β, y)的项，即尝试把y到x解析成B，已经解析了其中的α部分，接下来要解析A
      // 把(B -> α A • β, y)加入S[i]，表示尝试把y到i解析成B，已经解析了其中的α A部分
      (A -> γ •, x) => for (B -> α • A β, y) in S[x] { S[i].add((B -> α A • β, y)) }
    }
  }
}

最终如果S[N]中存在(Start -> γ •, 0)的话，就意味着整个输入串可以解析成γ，也就可以解析成Start，这个串被接受。反之则不接受。

看着这个代码，如果你熟悉Rust的话，肯定能反应过来一个问题：这样会出现迭代的过程中修改集合的操作，在Rust里肯定是不能通过编译的。Rust只是把这个问题暴露出来了，用别的语言的话也会遇到逻辑上的问题，例如我在执行S[i].add后，这个新加入的项后面迭代的时候会不会遇到？还有可能新加入的项满足之前的某个规则(注意complete规则中i可能等于x，所以有可能先执行了complete规则，之后才把一个这样的项加入S[i])，这样要不要重新考虑一遍之前执行的规则？

对于第一个问题，答案是for item in S[i]这个for会考虑后续加入的项，for (B -> α • A β, y) in S[x]这个for不考虑后续加入的项。迭代的过程用下标而非迭代器来写大概是这样的：

1
2
3
4
5
6
7
8
9
for (j = 0; j < S[i].len(); ++j) { // 每次len()都要重新读取
  item = S[i][j]
  // 这里的操作会增加S[i].len()
  // ...
  // for (B -> α • A β, y) in S[x]改写成
  for (k = 0, len = S[x].len(); k < len; ++k) { // 即使len变化，也不再考虑新加入的项了
    // i == x时这里会增加S[x].len()
  }
}

对于第二个问题，答案是原始的Earley算法不考虑，同时这也引入了下面的问题。

空规则

原始的Earley算法在处理存在可空的非终结符的语言时，可能会得到错误的结果。例如语言：

1
2
S -> A A
A ->

设开始符号是S，显然空串是这个语言的串。但是运行一下上面的算法，结果是：

1
2
3
4
=====S[0]=====
(S -> • A A, 0) # 初始化中加入
(A -> •, 0) # (S -> • A A, 0)，predicate规则
(S -> A • A, 0) # (A -> •, 0) & (S -> • A A, 0)，complete规则

到此为止了，S[0]中没有(S -> A A •, 0)，因此按照上面的算法，空串不被接受。其实这个时候如果再对(A -> •, 0)执行一次complete规则，因为(S -> A • A, 0)存在，所以会把(S -> A A •, 0)加入S[0]，这样就对了，但是原始的Earley算法中不会再考虑一次(A -> •, 0)。你可能会问是不是for (B -> α • A β, y) in S[x]这个for考虑后续加入的项就能解决问题呢？对上面这个语言确实是的，但是对这个语言，还是不行，所以这不是本质问题：

1
2
3
S -> A B A
A ->
B ->

考虑一下，发生这种情况的根本原因是什么？是因为complete规则中i = x，所以才需要纠结后续给S[i]新加入的项会不会影响到S[x]。什么情况下i = x？从x到i成功解析了A，而i = x，这意味着A是一个可空的非终结符。

论文Practical Earley Parsing中给出了一个解决方案：在predicate规则中加入一个操作：

1
2
3
4
5
6
7
8
9
...
// predicate规则
(A -> α • B β, x) => { 
  for (B -> γ) in grammar { S[i].add((B -> • γ, i)) } // 原本的操作
  // 新加入的操作
  // 因为B可空，所以不需要等到存在B -> γ •时才能把点移动过B，只要点在B左边就可以把它移动到右边
  if nullable(B) { S[i].add((A -> α B • β, x)) }
}
...

至于怎么计算每个非终结符是否可空，如果不追求效率的话就是很基本的自动机/编译原理的知识，相信大家都会。

上面的语言中，S和A都是可空的，运行一下修改后的Earley算法看看：

1
2
3
4
5
=====S[0]=====
(S -> • A A, 0) # 初始化中加入
(A -> •, 0) # (S -> • A A, 0)，predicate规则
(S -> A • A, 0) # (S -> • A A, 0)，predicate规则
(S -> A A •, 0) # (A -> •, 0) & (S -> A • A, 0)，complete规则

成功接受。

Earley parser

SPPF-Style Parsing From Earley Recognisers给出的方法是能够保证立方的复杂度的，可惜我看不太懂。http://loup-vaillant.fr/tutorials/earley-parsing/parser给出的方法很好理解，也比较好实现，但是他没有证明复杂度，我也没有能力和兴趣去证了。

基本思路就是从recognizer生成的表格中通过搜索得到树。首先把表格做一个类似转置的操作，方便后续分析：对于S[i]中的(A -> γ •, x)(只考虑点在最后的项，表示解析完成了)，在S'[x]中加入(A -> γ, i)(点可以忽略了，因为只加入了点在最后的项)，两者都是表示从x到i解析出γ。

已知S'[0]中存在(Start -> γ, N)，对于γ中的每一项，从第一项开始，它必须是从0开始解析的，看它是终结符还是非终结符，如果是终结符就把它和输入串中的对应位置进行匹配，如果不相等的话意味着这一支搜索失败了(第一项是不可能失败的，后面的项就有可能失败了)，相等的话就从1开始解析γ的第二项；如果是非终结符A，对于每个S'[0]的(A -> α, x)，分出一支进行搜索，因为它终止于x，所以之后就应该从x开始解析γ的第二项。

如此这样搜索下去，如果没有失败地考虑了γ的每一项，而且最终的结束位置等于N，这就是一支成功的搜索，表示成功地为S'[0]中的(Start -> γ, N)的每个孩子找到了一个产生它的项，接下来再继续对这些项进行类似的搜索即可，这个过程没有必要是递归的，可以把他们保存到队列里面，做广搜之类的，不然递归套递归可能有点难以理解。

SPPF

这些在上面的文章里没有，是我自己想到的。构思好了搜索的逻辑之后我很正常地想到搜索的过程中是不是可能出现相同的节点被多次搜索，比如：

1
2
3
4
5
6
7
8
9
S -> A B
A -> A1
A -> A2
A1 -> a
A2 -> a
B -> B1
B -> B2
B1 -> b
B2 -> b

按照上面描述的搜索，第一支是先搜A -> A1，再搜右端为B且从1开始解析的，第二支是先搜A -> A2，再搜右端为B且从1开始解析的，后面搜索的目标是一样的，也必然会得到相同的搜索结果，如果重复做一遍的话是一种浪费。

这其实就是朴素的SPPF(Shared Packed Parse Forest)的想法，它是用来高效表示有歧义的语法产生的多个语法树的数据结构。我没有找到它的官方定义或者是最先提出它的论文，所以我也不能确定我对它的理解是完全正确的，如果有错误的话麻烦大家及时指出。

SPPF是一个有向，可能有环的图，每个节点包含的信息有一个产生式和一段输入串，表示这段输入串可以按照这个产生式解析。每个节点连出一组边，每个边表示一组得到产生式右端式子的每一项的节点集。用我的程序输出上面的语法解析”a b”得到的SPPF是(我为了让它好看一点，做了一点修改)，一个圆圈连出的边就是这一组节点集：

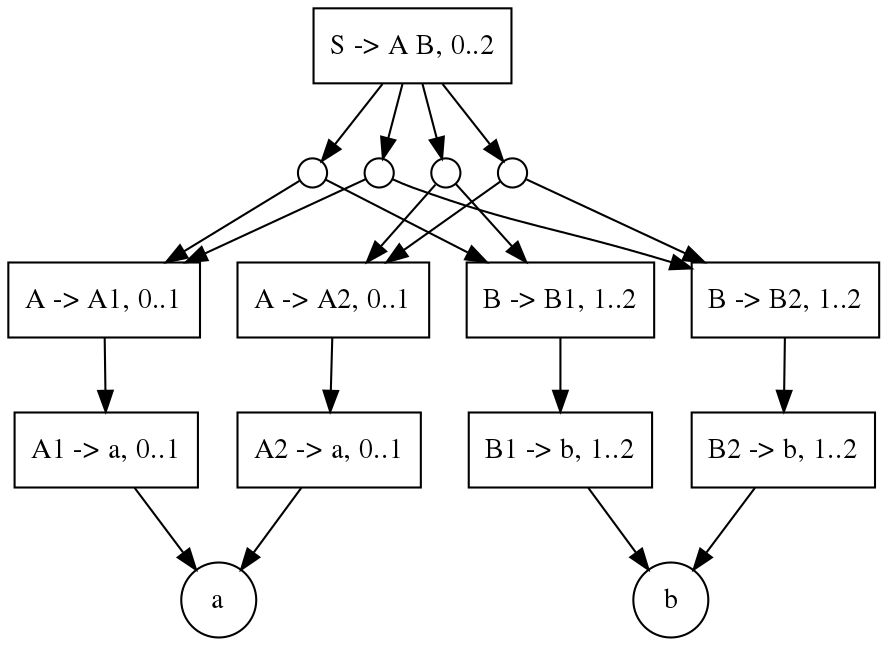
对上面描述的搜索算法做一点修改就可以生成SPPF，而不是一组树。对一个右端式子进行搜索，生成了一组合法的生成右端式子的组合时，将其中每个产生式和范围的元组加入一个集合中，得到一个id之类的东西保存起来，这样就把边连起来了，如果集合中已经存在这个产生式+范围的话就意味着出现了节点的重用。一次搜索结束后，继续对集合中未搜索的元组进行搜索(就是上面提到的广搜)。

除了节约空间之外，SPPF还带来了一个好处，因为它可以是有环的(这一定是因为存在可空的非终结符)，所以它可以表示无限多可能的语法树。例如这个语法：

1
2
A -> A
A ->

用它解析空串生成的SPPF是：

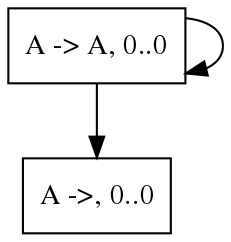
从SPPF到具体的树

到这里基本就跟Earley算法没有关系了，不过也算是parser的一部分。这个也花了我挺长时间的，看起来是一个比较正常的需求，但是找了半天也没有发现已经存在的算法，只能自己想了。其实也不算太复杂，但是毕竟我水平有限，还是想了一段时间才想出来。

首先想一个深搜的算法，搜索所有的树。这里有一个难点在于，每个节点往下可以有多个选择，每个选择中还有多个待搜索的节点，这就和简单的深搜不太一样了。主要还是要搞清楚访问节点的顺序是什么。以倒数第二张图为例，从S -> A B开始，首先选择最左边的圆圈(圆圈并不是具体的节点，而是表示一组节点)，然后往下走，先看A -> A1，需要搜索它的全部可能，比较幸运的是只有一个。继续往下走，到了a的时候停下，这个时候走完了这个分支，但是仍然没有为S -> A B构造一棵具体的树，因为B -> B1那一边还没有探索，所以需要能够从a这里跳到B -> B1继续搜索。

这个例子比较简单，但是也能看出来一点思路了：除了深搜的调用栈之外，还要再维护一个栈，每次选择一个产生式右端式子的一种可能时，只进入右端式子的第一项，而把剩余部分的信息保存到另一个栈中。当搜索进入一个叶子节点时，从这个栈中弹出一项，对它继续搜索；如果此时栈为空，即证明整个搜索已经完成。

然后把深搜的版本改造成一个基于栈+状态机的版本，这并不是为了性能或者防止爆栈，而是希望能给用户提供一个更便捷的接口，能够像访问迭代器一样访问所有可能的树。而且考虑到树的总数可能是无限的，这个转化就更重要了，理论上就不能用深搜构造一个容器来保存所有的树再把容器返回给用户。其实我之前还想过使用Rust的Generator，另一篇文章试用Rust的Generator其实就是为了这个写的，不过写完之后感觉现在的Generator还是不够成熟优雅，并不是很想用，还是自己转化成基于栈的版本吧。

这个其实就是机械的工作了，我一直都知道这是可行的，不过也没有尝试过，这次终于手动操作了一回，完成了之后还优化了好久才达到自己比较满意的样子。现在用户可以像这样生成树了：

1
2
3
4
5
6
let mut it = sppf.iter();
let mut cnt = 0;
while let Some(tree) = it.next() {
  std::fs::write(format!("{}.dot", cnt), format!("{}", tree)).unwrap();
  cnt += 1;
}

说点关于Rust的题外话。你可能会好奇我为什么不用Iterator::enumerate来实现类似的功能，其实是是因为it并没有实现Iterator。Iter::next的定义是：

1
2
3
4
5
6
7
8
9
pub struct Iter<'a> {
  ...
  tree: SPPF<'a>,
}

impl<'a> Iter<'a> {
  // 返回的树来自&self.tree，也用SPPF表示，不过保证每个节点只有一种选择，所以是确定的树
  fn next<'b>(&'b mut self) -> Option<&'b SPPF<'a>>;
}

比较遗憾的是这样的next不符合Iterator::next的要求，要让现在的Iter实现Iterator是不可能的，读者可以自己思考为什么。